Tilt Angle

The time has come to set the tilt angle for optimum power production. My final design allowed for a range of declination adjustment, but I deferred the complicated calculations until after the installation was complete. The results came as a surprise.

What you see below should be considered preliminary. I'm pretty sure it is accurate, but I need to spend more time with it to be certain I haven't erred somewhere.

The equation will be delayed until I find a Greek alphabet typeface. Request update notices.

This perspective view drawing identifies the angles and vectors that appear in the equation. It is shown in three views to help you gain the perspective.

Alpha = solar elevation angle (horizon = 0)
Psi = solar azimuth angle (east is -, south = 0, west is +)
Beta = array tilt angle (horizontal = 0)
Gamma = array rotation from true south
Theta = off-angle from normal solar incidence

View from the southeast

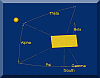
View from the south

View from the southwest

And here is the equation that describes the incident energy on the array surface as a function of many things - tilt angle in particular. The equation was initially derived from pure spherical trigonometry, and then compounded with a function to incorporate the extinction factor. In the process of researching extinction factors, another equation that presented a less-complicated approach was found in the literature. Some time was devoted to comparing the equations, and they appear to be equivalent. The simplified equation is presented here.

It ignores the unpredictables like fog and clouds. For these things we have capacity factor tables.

(Placeholder for the equation, someday)

If I were a solar zealot, and an early riser, I might go out to the array each morning before sunrise and adjust the tilt angle to receive the maximum possible energy for that day. To the right you'll see a plot of what that angle should be for each day of the year. You'll also see another plot (dashed line) that shows what the angle should be to receive the maximum possible energy at solar noon. Notice how the curves converge at the equinoxes.

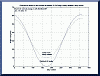Based on the above daily tilt settings, this plot shows the total incident energy for any day of the year. Integrating over the full year yields a total annual incident energy of 225 kWh per sq. ft.

I worried for quite a while about the humps and inflection points near the equinox days. Why is this curve not smooth?

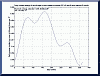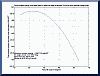
More realistically, I would be willing to adjust the tilt angle at least twice each year - say on each equinox. Here's a plot for the summer season of total incident energy vs. tilt angle. Maximizing the function yields the optimum angle of 12.14 degrees which would yield 115.5 kWh per sq. ft.

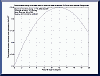Here is the continuation plot for the winter season, showing an optimum tilt angle of 51.06 degrees yielding 106.7 kWh per sq ft. Adding the total incident energy for the summer and winter seasons yields 222.2 kWh per sq. ft. - only slightly less than that of the solar zealot approach. I was really disappointed that there wasn't a bigger difference.

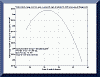
So maybe declination adjustment isn't so important after all. Here's what you get for a fixed position. Set and forget the array at the optimum angle of 31.09 degrees and receive 209.4 kWh per sq. ft. over the year.

I felt the need to perform a reality check to boost my confidence in these calculations.